其实是昨天上游戏引擎的课的时候旁边的同学给我看了这个图……

所以说啊,上课的时候不要搞这些有的没的,除非对扑克脸很有自信。
清明在即,除了提前挖个洞准备把自己埋起来之外,还是要准备一下ICPC昆明站……可是我们队里有大腿了,刷点网络流题验一验板子想必也是不错的。
大家最喜欢的网络流24题,到底能不能刷完呢——
P6000 – 搭配飞行员
这是一道经典的二分图匹配。
除了使用匈牙利算法之外,最大流也是可以解决这个问题的。
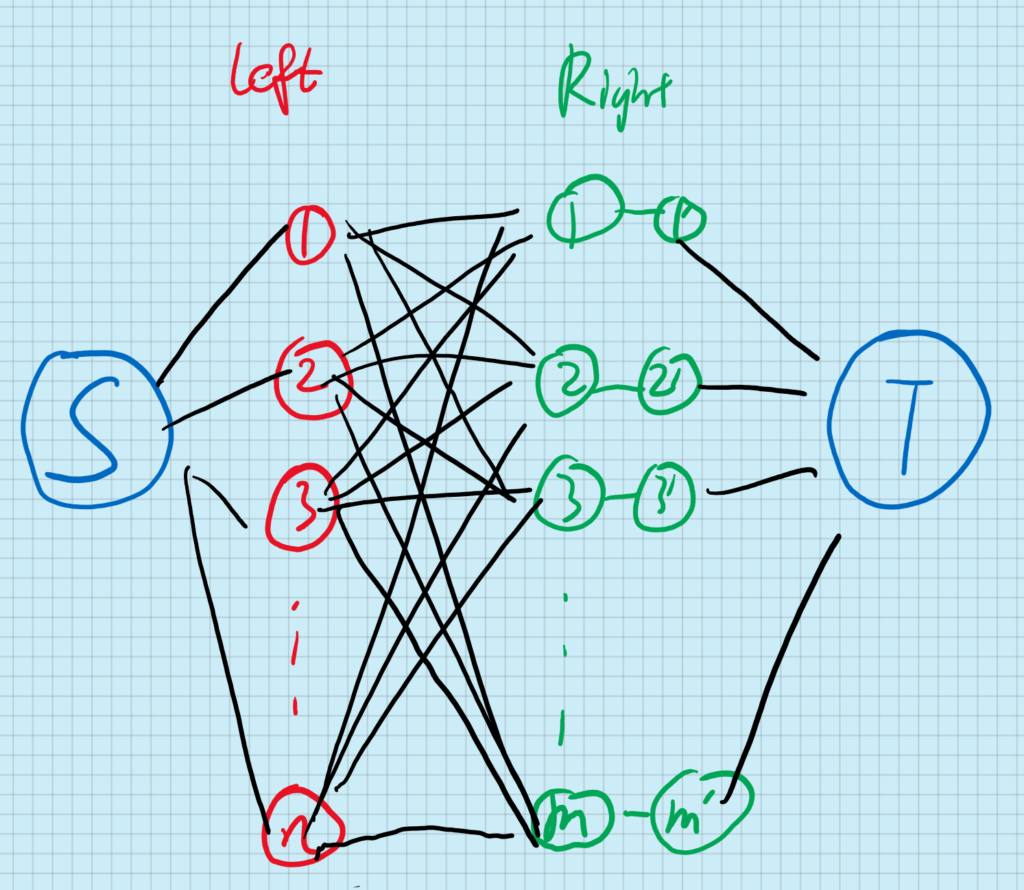
匈牙利算法的整体复杂度是 [latex]O(VE)[/latex] ,实际上会更小一点。
最大流(Dinic)的话可以把它降到 [latex]O(V \sqrt E)[/latex]。当然写还是前者更好写啦。
P6001 – 太空飞行计划
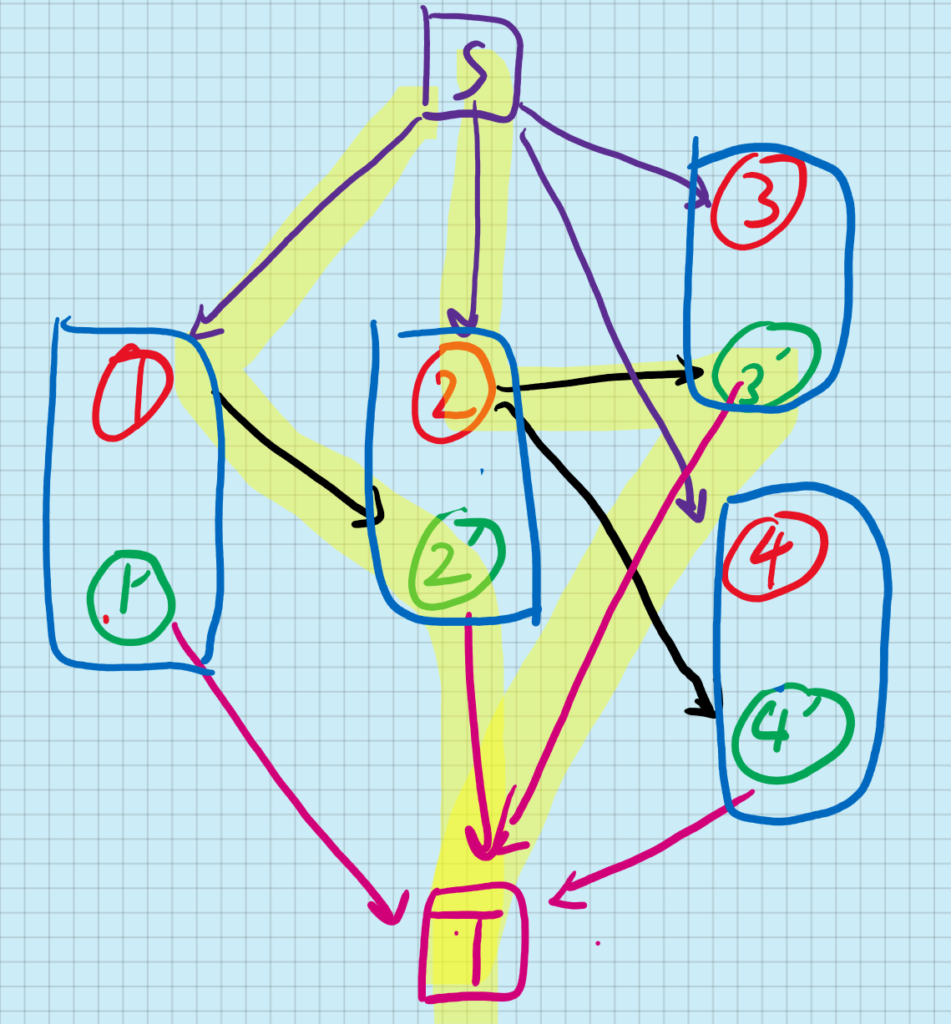
这题是一个最大权闭合子图,之前大概也写过三次(但不是三题)。
什么是闭合子图呢?和一个点相连的所有点也要在这个子图里,是谓闭合子图。最大权自然就是点全之和最大。
解法是对于正点权点,连S到它的边;对于负点权点,连它到T的边。流量取点权的绝对值。
对于原图的所有边,同样连边,流量取正无穷。
最大权值和 = 所有正点权之和 – 最小割,证明略。
网络流的割,就是把图切成两个子图使其不再连通。最小割就是切掉的边的权值和最小的割。
求最小割就是跑最大流。
如果只是这样的话,套板子也就过了,但是它要求输出方案。
那么我们可以跑完最大流之后从S开始DFS,给相连的点打上标记。所有和S相连的点,再加上所有和T不相连的点,就是所取的点。证明略。
(本菜鸡写证明略不是因为懒得写而是真的不会)
P6002 最小路径覆盖
路径……就是那么个路径;覆盖……就是若干条路径加起来能覆盖这个图。最小就是要让路径条数最少,并且本题中不允许顶点相交。
考虑最开始每个点自己单独一条路径,那么我们要做的就是把不同的路径连起来。每个点拆成两个点之后(这两个点不连边)照原图建图,跑二分图最大匹配:每匹配到一条边,路径总数就减少1。
跑完最大流之后回去看看哪些正向边的flow是0,这些就是我们的最终方案中包含的边。
